Kantdetekteringsfilter söker kanter mellan olika färger och kan därmed identifiera konturer för objekt.

De används för att göra markeringar och för många konstnärliga syften.

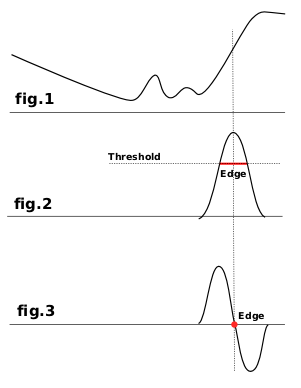
De flesta av dem baseras på gradientberäkningsmetoder och ger tjocka kantlinjer. Se på figur 1 som representerar variationer i färgintensitet. Till vänster är en långsam färggradient som inte är en kant. Till höger är en snabb variation som är en kant. Låt oss nu beräkna gradienten, variationshastigheten, av denna kant, d.v.s. förstaderivatan (figur 2). Vi behöver bestämma att en kant identifieras när gradienten är mer än ett tröskelvärde (den exakta kanten är högst upp i kurvan, men denna topp varierar enligt kanter). I de flesta fall är tröskelvärdet under toppen och kanten är tjock.

Laplace-kantdetektering använder andraderivatan (figur 3). Toppen på kurvan är nu på noll och tydligt identifierad. Därför renderar Laplace-filtret en tunn kant, bara en bildpunkt bred. Men denna derivata ger flera nollor motsvarande små krusningar, vilket resulterar i falska kanter.

Viss oskärpa före kantfilter tillämpas är ofta nödvändig: det plattar ut små signalkrusningar och förhindrar därför falska kanter.