| 9.2. Faltungsmatrix | ||
|---|---|---|

|
9. Allgemein |  |
Dies ist eher die Domäne von Mathematikern, denn die meisten Filter verwenden eine Faltungsmatrix. Mit dem Faltungsmatrix-Filter können Sie, Fantasie vorausgesetzt, ein eigenes Filter bauen.
Was ist nun aber eine Faltung? Eine ungefähre Vorstellung können Sie auch ohne die mathematischen Werkzeuge bekommen, die nur wenigen Eingeweihten zugänglich sind: Eine Faltung ist eine Anwendung einer Matrix auf eine andere, die „Kern“ genannt wird.
Das Faltungsmatrix-Filter verwendet eine erste Matrix, auf welche das Bild angewendet wird. Das Bild ist eine zweidimensionale Pixelmenge in einem rechtwinkligen Koordinatensystem. Der verwendete Kern hängt vom gewünschten Ergebnis ab.
GIMP verwendet als Kern Matrizen mit 5x5 oder 3x3 Einträgen. Hier werden nur 3x3-Matrizen betrachtet, da diese weiter verbreitet sind und die wesentlichen Effekte mit ihnen realisiert werden können. Wenn alle Kantenwerte des Kerns auf Null gesetzt sind, geht das System davon aus, dass es sich um eine 3x3-Matrix handelt.
Das Filter betrachtet nacheinander jedes Pixel des Bildes. Für das aktive Pixel, das wir hier „Initialpixel“ nennen wollen, und seine 8 Nachbarpixel wird eine Multiplikation mit den entsprechenden Elementen des Kernes durchgeführt. Die Ergebnisse dieser Multiplikationen werden aufsummiert und als neuer Wert des Initialpixels übernommen.
Die nachfolgende Abbildung verdeutlicht den Ablauf:
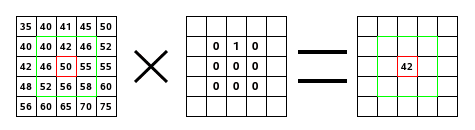
Auf der linken Seite sehen Sie das Bild, als Matrix dargestellt. Die Farbwerte werden durch Zahlen repräsentiert. Das aktuell bearbeitete Pixel ist rot umrandet. Der Bereich, auf den der Kern angewendet wird, ist grün umrandet. In der Mitte des Bildes sehen Sie den Kern. Auf der rechten Seite das bearbeitete Pixel nach Anwendung des Kerns, also das Ergebnis der Faltung.
Was ist nun genau passiert? Das Filter liest, von links nach rechts, Zeile für Zeile alle Werte des Bereiches, auf das der Kern angewendet wird. Dabei werden die Werte der Bildmatrix mit den korrespondierenden Werten des Kerns multipliziert und die Ergebnisse addiert. Welchen Wert erhält also das aktuell bearbeitete Pixel? Nun, die Antwort ist 42: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42. (Natürlich führt das Filter die Berechnungen mit Hilfe einer Kopie durch). Das sichtbare Ergebnis bei diesem Kern ist, dass jedes Pixel eine Position nach unten verschoben wird.
![[Anmerkung]](images/note.png)
|
Anmerkung |
|---|---|
|
These options are described in Abschnitt 2, „Gemeinsame Funktionsmerkmale“. |
Dies ist die 5x5-Matrix, der Kern. Sie können die gewünschten Werte direkt in die Eingabefelder eintragen.
The result of previous calculation will be divided by this divisor. You will hardly use anything else than 1, which leaves results unchanged, and 9 or 25 according to matrix size, which gives the average of pixel values. The divisor can only be changed when Normalize is unchecked.
This value is added to the division result. This is useful if result may be negative. This offset may be negative. It can only be changed when Normalize is unchecked.
Here you can select which channels the filter should change.
Wenn diese Eigenschaft des Filters aktiviert ist, werden die Werte für Divisor und Versatz automatisch optimal gewählt.
Wenn diese Eigenschaft nicht aktiviert ist, wird ein im Bild vorhandener Alphakanal nicht in die Berechnung einbezogen. Dies kann zu Artefakten im Bild führen, wenn eine Weichzeichnung durch die Faltungsmatrix vorgenommen wird.
Wenn sich das aktuell bearbeitete Pixel am Rand des Bildes befindet, ist ein Teil des Kernes außerhalb des Bildes. Sie können einstellen, wie sich das Filter in einem solchen Fall verhält:




From left: source image, None border, Loop border, Clamp border
Dieser Teil des Kernes wird nicht berücksichtigt.
Dieser Teil des Kernes betrachtet die Pixel auf der gegenüberliegenden Seite des Bildes.
Die Pixel am Rand werden nicht bearbeitet und abgeschnitten.
Pixels on borders are changed to black.
Pixels on borders are changed to white.
Der Entwurf von Kernen erfordert spezielle mathematische Kenntnisse. Die folgenden Beispiele enthalten Kerne, die Sie ausprobieren können, auch wenn Sie kein Diplom in höherer Mathematik erworben haben: