| 9.2. Faltningsmatris | ||
|---|---|---|

|
9. Generiska filter |  |
Här är en domän för matematiker. De flesta filter använder en faltningsmatris. Med filtret Faltningsmatris kan du, om andan faller på, bygga ett anpassat filter.
Vad är en faltningsmatris? Det är möjligt att få en grov uppfattning av det utan att använda matematiska verktyg som bara några få känner till. Faltning är behandlingen av en matris med en annan som kallas ”nollrum” eller kärna.
Filtret Faltningsmatris använder en första matris som är bilden som ska behandlas. Bilden är en tvådimensionell samling bildpunkter i rektangulära koordinater. Nollrummet som används beror på effekten som du vill ha.
GIMP använder matriser av storleken 5×5 eller 3×3. Vi kommer enbart titta på 3×3-matriser, de används mest och är tillräckliga för alla effekter som du vill ha. Om alla kantvärden för ett nollrum sätts till 0 så kommer systemet anse det vara en 3×3-matris.
Filtret studerar i tur och ordning varje bildpunkt i bilden. För var och en av dem, vilka vi kallar den ”ursprungliga bildpunkten”, multiplicerar det värdet på denna bildpunkt och värden för de 8 omkringliggande bildpunkterna med nollrummets motsvarande värde. Det lägger sedan ihop resultaten, och den ursprungliga bildpunkten ställs in till detta slutgiltiga resultatvärde.
Ett enkelt exempel:
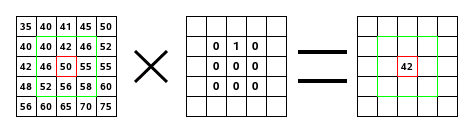
Till vänster är bildmatrisen: varje bildpunkt är markerad med sitt värde. Den ursprungliga bildpunkten har en röd kant. Nollrummets åtgärdsområde har en grön kant. I mitten är nollrummet, och till höger är faltningens resultat.
Här är vad som hände: filtret läste i tur och ordning, från vänster till höger och uppifrån och ner, alla bildpunkter i nollrummets åtgärdsområde. Det multiplicerade värdet av var och en av dem med nollrummets motsvarande värde och adderade resultaten. Den ursprungliga bildpunkten har blivit 42: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42. (Filtret arbetar inte på bilden utan på en kopia). Som grafiskt resultat har den ursprungliga bildpunkten flyttat ner en bildpunkt.
![[Notera]](images/note.png)
|
Notera |
|---|---|
|
Dessa alternativ beskrivs i Avsnitt 2, ”Gemensamma funktioner”. |
Detta är 5×5-nollrumsmatrisen: du matar in önskade värden direkt i rutor.
Resultatet av föregående beräkning kommer divideras med denna nämnare. Du kommer sällan använda något annat än 1, vilket lämnar resultat oförändrade, och 9 eller 25 beroende på matrisstorlek, vilket ger medelvärdet av bildpunktsvärden. Nämnaren kan endast ändras när Normalisera ej är ikryssat.
Detta värde adderas till divisionens resultat. Detta är användbart om resultatet kan vara negativt. Denna position kan vara negativ. Den kan endast ändras när Normalisera ej är ikryssat.
Här kan du välja vilka kanaler som filtret ska ändra.
Om detta alternativ är ikryssat tar nämnaren resultatvärdet av faltningen. Om detta resultat är lika med noll (division med noll är omöjligt) så tillämpas en position på 128. Om det är negativt (en negativ färg är omöjlig) så tillämpas en position på 255 (inverterar resultat).
Om detta alternativ inte är ikryssat tar filtret inte transparens i beaktande och det kan vara orsaken till vissa störningar när bilden görs oskarp.
När den ursprungliga bildpunkten är på en kant är en del av nollrummet utanför bilden. Du måste bestämma vad filtret ska göra:




Från vänster: källbild, Inget, Slinga, Begränsa
Denna del av nollrummet tas inte i beaktande.
Denna del av nollrummet kommer studera bildpunkter på motsatt kant, så bildpunkter som försvinner från en sida dyker upp igen på den andra sidan.
Bildpunkter på kanter ändras inte, men beskärs.
Bildpunkter på kanter ändras till svart.
Bildpunkter på kanter ändras till vitt.