Les filtres de détection des bords recherchent les limites entre les couleurs et détectent ainsi le contour des objets.

Ils sont utilisés pour créer des sélections et dans de multiples effets artistiques.

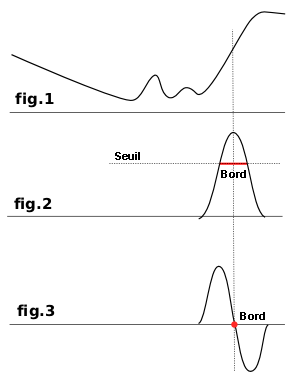
La plupart d’entre eux sont basés sur des méthodes de calcul de gradient et donnent des bordures épaisses. Considérez la figure 1 qui représente des variations d’intensité de couleur. Sur la gauche se trouve un lent dégradé de couleur qui n’est pas un bord. Sur la droite, une brusque et importante variation est un bord. Maintenant, calculons la pente, la vitesse de variation, de ce bord : c’est la dérivée première (fig.2). Nous devons décider qu’un bord est détecté quand la pente dépasse un certain seuil (le bord se trouve exactement au sommet de la courbe mais on ne peut l’utiliser car son niveau varie selon les bords). Dans la plupart des cas, le seuil se trouve en dessous du sommet et le bord est épais.

Le filtre de Laplace utilise la dérivée seconde (fig.3). Le sommet se retrouve a zéro et est nettement identifié. C’est pourquoi ce filtre donne une bordure fine, de 1 pixel. Mais ce calcul donne aussi plusieurs autres zéros correspondant aux petites rides du signal, ce qui est cause de multiples faux bords dans l’image.

Donner un peu de flou à l’image avant d’appliquer un filtre de détection de bords est souvent nécessaire pour éviter ces faux bords.