| 9.2. Matriz de convolución | ||
|---|---|---|

|
9. Filtros genéricos |  |
Es un dominio de matemáticos. La mayoría de los filtros usan una matriz de convolución. Con el filtro «matriz de convolución», si tiene imaginación, puede crear filtros personalizados.
¿Que es una matriz de convolución? Es posible hacerse una idea sin usar las herramientas matemáticas que sólo conocen unos pocos. Convolución es el tratamiento de una matriz por otra que se llama “kernel”.
El filtro matriz de convolución usa una primera matriz que es la imagen que será tratada. La imagen es una colección bidimensional de píxeles en coordenada rectangular. El kernel usado depende del efecto deseado.
GIMP usa matrices 5x5 o 3x3. Se considerarán sólo las matrices 3x3, son las más usadas y son suficiente para los efectos deseados. Si todos los valores del borde de un kernel se seleccionan a cero, el sistema la considerará como una matriz 3x3.
El filtro examina, sucesivamente, cada píxel de la imagen. Para cada uno de ellos, que se llamará “píxel inicial”, se multiplica el valor de este píxel y los valores de los 8 circundantes por el valor correspondiente del kernel. Entonces se añade el resultado, y el píxel inicial se regula en este valor resultante final.
Un ejemplo simple:
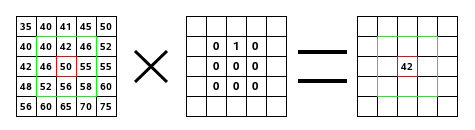
A la izquierda, la imagen de la matriz: cada píxel está marcado con su valor. El píxel inicial tiene un borde rojo. El área de acción del kernel tiene un borde verde. En el medio, el kernel, y a la derecha, el resultado de convolución.
Lo que sucede aquí: el filtro lee sucesivamente, de izquierda a derecha y de arriba a abajo, todos los píxeles del área de acción del kernel. Se multiplica el valor de cada uno de ellos por el valor correspondiente del kernel y se suman los resultados. El píxel inicial llega a 42: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42. (el filtro no trabaja sobre la imagen sino sobre una copia). Como resultado gráfico, el píxel inicial se movió un píxel hacia abajo.
![[Nota]](images/note.png)
|
Nota |
|---|---|
|
Estas opciones se describen en la Sección 2, “Características comunes”. |
Es una matriz kernel de 5x5: el valor se introduce directamente en las cajas.
El resultado del cálculo anterior se dividirá por este divisor. Difícilmente utilizará otro número que no sea 1, lo que deja los resultados sin cambios, y 9 o 25 según el tamaño de la matriz, que da la media de los valores de píxel. El divisor solo se puede cambiar cuando Normalizar no está marcado.
Este valor se suma al resultado de la división. Es útil si el resultado es negativo. Este desplazamiento puede ser negativo. Solo se puede cambiar cuando Normalizar no está marcado.
Aquí puede seleccionar qué canales cambiará el filtro.
Si esta opción está marcada, el divisor toma el valor resultante de la convolución. Si este resultado es cero (no es posible dividir por cero), se aplica un desplazamiento de 128. Si es negativo (un color negativo no es posible), se aplica un desplazamiento de 255 (se invierte el resultado).
Si esta opción no está marcada, el filtro no tiene en cuenta la transparencia y esto puede producir algunos artefactos cuando se desenfoca.
Cuando el píxel inicial está sobre un borde, una parte del kernel se sitúa fuera de la imagen. Puede decidir qué filtro debe usar:




Desde la izquierda: imagen original, borde Ninguno, borde Bucle, borde Abrazadera
Esta parte del kernel no se tiene en cuenta.
Esta parte del kernel examinará los píxeles del borde opuesto, así que los píxeles desaparecidos por un lado reaparecen por el otro lado.
Los píxeles sobre los bordes no se modifican, pero sí se recortan.
Los píxeles sobre los bordes se cambian a negro.
Los píxeles sobre los bordes se cambian a blanco.