Filtry detekce hran hledají v obrázku hranice mezi jednotlivými barvami, tedy obrysy grafických prvků, ze kterých se obrázek skládá.

Hodí se při tvorbě výběrů a k různým uměleckým záměrům.

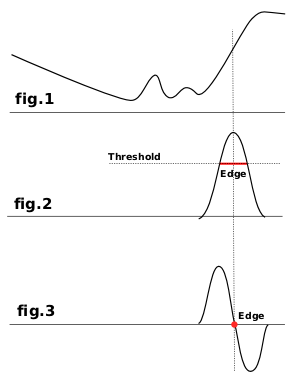
Most of them are based on gradient calculation methods and give thick border lines. Look at fig.1 which represents color intensity variations. On the left is a slow color gradient which is not a border. On the right is a quick variation which is an edge. Now, let us calculate the gradient, the variation speed, of this edge, i.e. the first derivative (fig.2). We have to decide that a border is detected when gradient is more than a threshold value (the exact border is at top of the curve, but this top varies according to borders). In most cases, threshold is under top and border is thick.

Laplaceova metoda hledání hran používá druhou derivaci (graf 3). Hledaná část křivky protíná nulovou hodnotu a je tedy jasně definovaná. Proto Lapalceova metoda vede k tenkým jednopixelovým hranám. Druhá derivace však také nabývá nulových hodnot na mnoha místech, kde dochází k malým nepravidelnostem, výsledkem jsou falešné hrany.

Vzniku falešných hran lze zabránit mírným rozostřením obrázku před použitím Laplaceova filtru. Drobné nepravidelnosti se rozostří, a tak se zabrání vzniku falešných hran.