Edge detect filters search for borders between different colors and so can detect contours of objects.

They are used to make selections and for many artistic purposes.

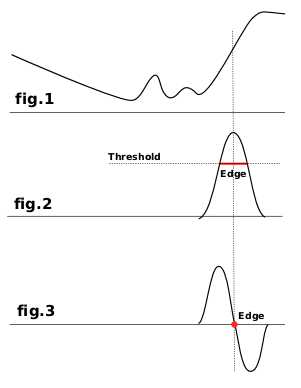
Most of them are based on gradient calculation methods and give thick border lines. Look at fig.1 which represents color intensity variations. On the left is a slow color gradient which is not a border. On the right is a quick variation which is an edge. Now, let us calculate the gradient, the variation speed, of this edge, i.e. the first derivative (fig.2). We have to decide that a border is detected when gradient is more than a threshold value (the exact border is at top of the curve, but this top varies according to borders). In most cases, threshold is under top and border is thick.

The Laplacian edge detection uses the second derivative (fig.3). The top of the curve is now at zero and clearly identified. That's why Laplace filter renders a thin border, only a pixel wide. But this derivative gives several zeros corresponding to small ripples, resulting in false edges.

Some blurring before applying edge filters is often necessary: it flattens small ripples in signal and so prevents false edges.