| 14.4. Fractal IFS | ||
|---|---|---|

|
14. Filtres de renderització |  |
Aquest connector basat en fractals és realment meravellós. Amb aquesta eina versàtil es pot crear formes naturals orgàniques com ara fulles, flors, branques o fins i tot arbres. El nom original del connector és IFS, un acrònim d'«Iterated Function System».
La clau per utilitzar aquest connector és fer moviments petits i precisos en l'espai de la fractal. El resultat és difícil de predir, i cal tenir molta cura quan canvieu el patró. Si feu un component en forma de triangle massa gran, o si ho moveu massa lluny (encara que sigui lleugerament), la pantalla de la previsualització s'apagarà, o, amb més freqüència, tindreu un núvol de partícules amorfes.
Un consell: quan trobeu un patró amb el qual vulgueu treballar, feu només petits canvis i exploreu les variacions d'aquest patró. És molt fàcil perdre una bona configuració. Contràriament al que pugueu creure, és més fàcil crear una fulla o un arbre amb la Composició IFS que crear un patró geomètric específic.
Per a una introducció ràpida a l'IFS consulteu Foley i van Dam Computer Graphics, Principles and Practice[FOLEY01].
La interfície del connector consisteix en una zona de composició a l'esquerra, una pantalla de la previsualització a la dreta, i algunes pestanyes i botons d'opcions a sota. La configuració per defecte consisteix amb tres triangles equilàters (això es coneix com a Triangle de Sierpinski).
Barra d'eines
Feu clic als botons de la barra d'eines, o obriu el menú contextual fent clic dret a l'àrea de composició.
Seleccioneu l'acció a realitzar amb el punter del ratolí.
Afegeix o elimina les fractals.
Estàndard.
Enllaça les fractals i permet aplica'ls-hi accions a tots.
Recalcula el centre de les fractals. No té un efecte visible en el fractal resultant.
Permet accelerar el renderitzat. És especialment útil quan es treballa amb un radi de punt elevat; recordeu d'utilitzar múltiples del valor per defecte: 4096, 8192, 16384, ...
Determina el nombre de vegades que el fractal es repetirà, (un valor alt per a les subdivisions d'iteracions és per raons òbvies una pèrdua de temps del procés, a no ser que la imatge sigui molt gran).
Controla el nivell de detall.
Determina la densitat de les «pinzellades» en la imatge renderitzada. Un radi petit és bo pels núvols de partícules fines o polvoritzades, mentre que un radi gran produeix pinzellades gruixudes, un color sòlid com d'aquarel·la. Tingueu cura de no utilitzar un radi massa gran, ja que caldria molt de temps de renderització.
Us dona informació de la fractal actiu, i permet posar un valor en comptes de canviar-lo amb el ratolí, que no és gaire precís. Per tant, és una opció útil quan us cal precisió.
Mou, ajusta la mida, o talla el fractal actiu.
Estira el fractal actiu.
Capgira el fractal actiu.
Transformació del color
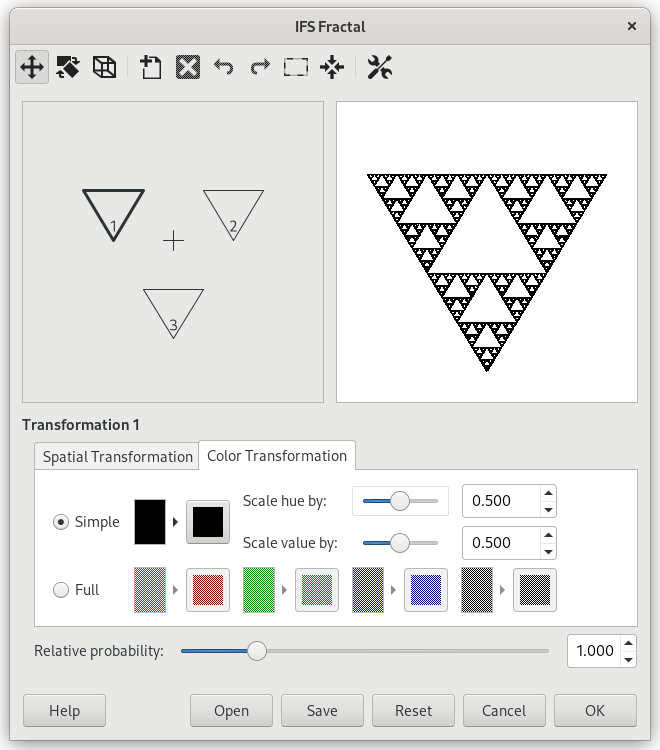
Canvia el color del component actiu de la fractal per un altre que seleccioneu (per defecte utilitza el color del primer pla de la caixa d'eines).
Com en la transformació de color simple, però aquesta vegada podeu gestionar la transformació per a cada canal de color i per al canal alfa (representat com un canal negre).
Quan teniu molts fractals amb diferents colors, els colors es barregen. Així que si establiu un «vermell pur» per a un fractal, podria quedar blau en alguna part, mentre que un altre fractal «vermell» podria tenir groc. L'escala to/valor canvia la intensitat del color del fractal actiu, o marca quina influència del color de la fractal hauria de ser.
Altres
Determina la influència o l'impacte total d'un fractal determinat.
És un connector bastant complex, així que per a ajudar-vos a entendre'l, us guiarem a través d'un exemple on creareu una fulla o una branca.
Moltes formes de vida, i especialment les plantes, estan construïdes com a fractals matemàtics, és a dir, una forma que reprodueix o es repeteix a si mateixa indefinidament en detalls més petits. Fàcilment podeu reproduir la forma d'una fulla o una branca utilitzant quatre o més fractals. Tres fractals donen forma a la punta i les vores de la fulla i el quart representa la tija.
Abans d'activar el filtre: seleccioneu → Afegeix una capa transparent amb → → . A la caixa d'eines, establiu el color del primer pla: negre, i el color del fons: blanc.
Obriu el filtre Fractal IFS. Comenceu amb una rotació dels triangles dret i inferior, perquè apuntin cap amunt. Ara, podreu veure el contorn del qual serà la punta i els costats de la fulla. (Si teniu problemes, us podria ajudar saber que els tres vèrtexs de cada triangle no són pas equivalents).
Figura 17.335. 2n pas del tutorial
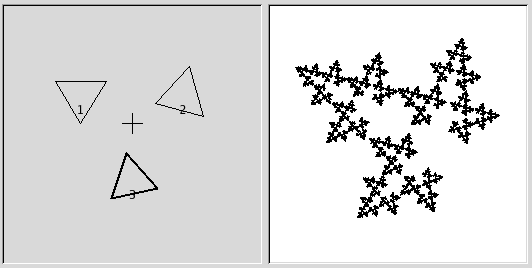
Comenceu per una rotació dels triangles 2 i 3, i tracteu de mantenir-los gairebé en la mateixa mida.
Per a fer la fulla simètrica, ajusteu el triangle inferior perquè apunti lleugerament a l'esquerra, i el triangle dret que apunti lleugerament a la dreta.
Premeu per a afegir un component a la composició. Serà la tija de la fulla, així que necessitareu fer-la llarga i fina. Feu clic a , i arrossegueu fins a estirar el nou triangle. No us alarmeu si es fa malbé la imatge, utilitzeu l' per a ajustar la mida del triangle massa llarg. Probablement, també s'haurà de moure i girar el fractal nou perquè sembli convincent.
Figura 17.336. 3r pas del tutorial
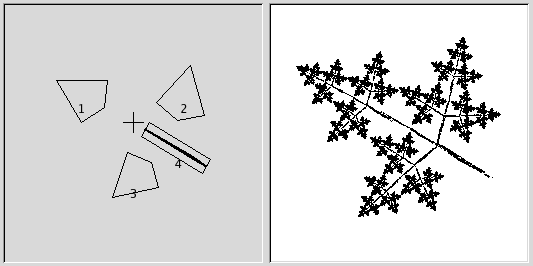
Afegiu un quart component, i després l'estireu, li canvieu la mida i el moveu tal com està indicat.
Encara heu de fer que s'assembli més a una fulla. Incrementeu la mida del triangle superior, fins que es vegi prou gruixut i frondós. Ajusteu tots els fractals fins a aconseguir la forma desitjada. Feu clic dret perquè aparegui el menú, i trieu . Ara tots els components estan seleccionats, i podeu canviar la mida i girar la fulla sencera.
Figura 17.337. 4t pas del tutorial

Allargueu el component 1, arregleu de manera adequada els altres components, després seleccioneu-ho tot, canvieu la mida i gireu.
El pas final és ajustar el color. Feu clic sobre la pestanya , i trieu un color diferent per a cada fractal. Per a fer això, marqueu i feu clic a sobre el quadre de color de la dreta. Apareix un cercle de color on s'hi pot fer clic o també s'hi pot seleccionar un color.
Figura 17.338. 5è pas del tutorial

Assigneu un color marró al component 4 i diversos matisos de verd pels altres components.
Feu clic a D'acord, i heus ací, s'acaba de fer una fulla fractal perfecta. Ara que ja ho heu après, podeu experimentar i fer els vostres dissenys. Totes les fractals imiten plantes (ja siguin roures, falgueres o palla) i estan fetes més o menys d'aquesta manera: al voltant d'una tija (o vàries). Per a obtenir una planta totalment diferent, només cal que l'estireu i el gireu una mica o li afegiu uns pocs fractals.