| 8.2. Matriz de convolução | ||
|---|---|---|

|
8. Filtros genéricos |  |
Este é um domínio dos matemáticos. Um grande número de filtros usa a matriz de convolução internamente - como os de desfocagem, nitidez, mapa de relevo, dentre outros. Com o filtro de matriz de convolução, se tiver imaginação para tal, você poderá criar um filtro personalizado.
O que é uma matriz de convolução? É possível ter uma ideia melhor disso sem precisar usar ferramentas matemáticas usadas por poucas pessoas. Convolução é o tratamento de uma matriz por outra chamada “núcleo” (kernel).
O filtro de Matriz de Convolução usa uma matriz primária, que é a imagem a ser tratada. Essa imagem é tratada como uma coleção bi-dimensional de pixels em coordenadas retangulares. O núcleo a ser usado vai depender do efeito desejado.
O GIMP usa matrizes 5x5 ou 3x3. Nós consideraremos aqui apenas matrizes 3x3, elas são as mais usadas e são o bastante para quase todos os efeitos que você desejar fazer. Se todos os valores das bordas de um kernel 5x5 forem marcados em zero, então o sistema irá considera-lo como uma matriz 3x3.
O filtro analisa cada pixel da imagem sucessivamente. Para cada um deles, que nós vamos chamar de “pixel inicial”, o valor desse pixel será multiplicado pelo valor dos 8 pixels ao redor do mesmo pelo valor correspondente na matriz núcleo. Esses nove valores são adicionados e se tornam o valor final daquele pixel. Esta operação é feita em cada um dos canais de cor, no caso de uma imagem RGB(A).
Um exemplo simples:
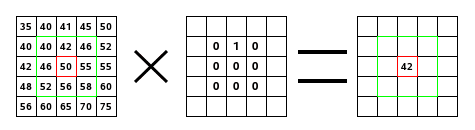
Na imagem da esquerda está a imagem matriz: cada pixel com seu valor próprio. O pixel inicial está entre as bordas vermelhas. O núcleo atua na área com bordas verdes. Na imagem do meio está o núcleo, e a direita é o resultado da convolução.
Isso é o que acontece: o filtro lê sucessivamente, da esquerda para a direita e de cima para baixo, todos os pixels da área de ação do núcleo. Ele multiplica o valor de cada um deles pelo valor correspondente do núcleo e depois soma os resultados. O pixel inicial se tornou um 42: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42. (o filtro não trabalha diretamente sobre a imagem, mas sim em uma cópia). Para o resultado ser visível, o pixel inicial foi movido para baixo do pixel resultante.
Essa é a matriz 5x5 do kernel: você digita os valores desejados diretamente nas caixas de texto.
O resultado do calculo anterior será divido pelo número inserido. Você mais frequentemente usará o valor 1, que não vai mudar o resultado da soma, ou 9 ou 25 de acordo com o tamanho da matriz, o que resultará na média dos valores dos pixels.
O valor adicionado será adicionado ao resultado da divisão. Isso é muito útil caso o resultado possa ser negativo. Você pode adicionar um valor de deslocamento negativo.
Quando o pixel inicial se localizar na borda da imagem, uma parte do núcleovai ficar fora da imagem. Você deve decidir se o filtro deve:




A partir da esquerda: imagem original, Estender a borda, Dar a volta na borda, Cortar borda.
Esta parte do núcleo não será levada em conta.
Esta parte do núcleo vai examinar os pixels da borda oposta, o que fará com que pixels desapareçam de um lado e reapareçam do outro.
Os pixels das bordas não serão modificados, mas sim recortados.
Você selecionar em quais canais o filtro vai operar.
Se esta opção estiver marcada, o Divisor pegará o valor resultante da convolução. Se o resultado for zero (não é possível dividir por zero), então um valor de deslocamento de 128 será aplicado. Se ele for negativo (um valor de cor negativo não existe), então um valor de deslocamento de 255 será aplicado (o resultado será invertido).
Se esta opção não estiver marcada, então o filtro não levará em conta os valores do canal de transparência, o que pode criar alguns artefatos durante o processamento.
A criação de núcleos é baseada em conhecimentos matemáticos, ou de ciência da computação, de alto nível. Você pode encontrar núcleos prontos na internet (procure pela expressão em inglês: “Convolution kernel”). Veja alguns exemplos: